Big O and Algorithm Efficiency
Big O Notation & Algorithmic Efficiency
Overview
Understanding how algorithms perform as input size grows is crucial. We use Big O notation to describe their efficiency. Big O notation helps us analyze:
- Time Complexity: How runtime increases with input size.
- Space Complexity: How much extra memory is needed.
What is Big O?
Big O notation expresses the worst-case scenario runtime of an algorithm. It provides an upper bound on how an algorithm behaves as the input size grows.
Common Big O Complexities
| Complexity | Name | Example |
|---|---|---|
| O(1) | Constant | arr[0] |
| O(log n) | Logarithmic | Binary Search |
| O(n) | Linear | Loop through an array |
| O(n log n) | Linearithmic | Merge Sort |
| O(n²) | Quadratic | Nested loops |
| O(2ⁿ) | Exponential | Recursive Fibonacci |
| O(n!) | Factorial | Permutations |
Brief Video: https://www.youtube.com/watch?v=g2o22C3CRfU
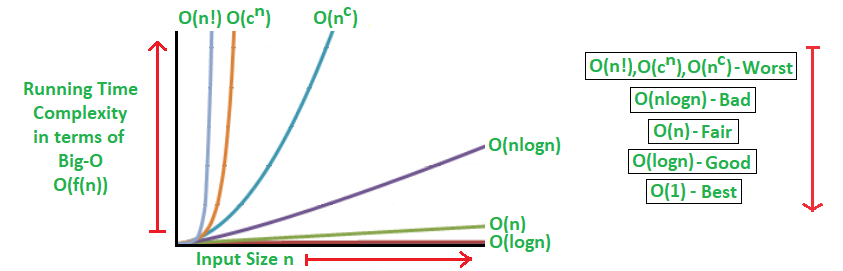
Examples & Explanations
Constant Time – O(1)
def get_first_element(arr):
return arr[0]
Takes the same amount of time, regardless of input size.
Even if arr has 1 or 1,000,000 elements, this function always runs in one step.
Linear Time – O(n)
def print_elements(arr):
for item in arr:
print(item)
Time grows proportionally with input size.
If arr has 5 elements, we run the loop 5 times. If it has 1,000 elements, we run it 1,000 times.
Quadratic Time – O(n²)
def print_pairs(arr):
for i in range(len(arr)):
for j in range(len(arr)):
print(arr[i], arr[j])
As n grows, operations increase quadratically.
If arr has 10 elements, we perform 100 operations. If it has 100 elements, we perform 10,000 operations.
Logarithmic Time – O(log n)
def binary_search(arr, target):
left, right = 0, len(arr) - 1
while left <= right:
mid = (left + right) // 2
if arr[mid] == target:
return mid
elif arr[mid] < target:
left = mid + 1
else:
right = mid - 1
return -1
Efficient for searching in sorted data.
Each step cuts the input size in half. Searching in 1,000,000 elements takes ~20 steps instead of 1,000,000.
Exponential Time – O(2ⁿ)
def fibonacci(n):
if n <= 1:
return n
return fibonacci(n - 1) + fibonacci(n - 2)
Very slow for large n.
For n = 10, this function does ~1000 calls. For n = 50, it does billions of calls.
Real-World Analogies
Utilizing everyday scenarios can make abstract Big O concepts more relatable:
-
O(1) – Constant Time Complexity: Imagine a vending machine where pressing a button dispenses a snack immediately, regardless of the number of snacks inside. Similarly, an algorithm with O(1) complexity performs its task in constant time, irrespective of input size. MBLOGING
-
O(n) – Linear Time Complexity: Consider searching for a specific book in an unsorted stack by examining each one sequentially. The time taken grows linearly with the number of books, analogous to O(n) complexity.
-
O(n²) – Quadratic Time Complexity: Think about organizing a round-robin tournament where each participant competes against every other participant once. As the number of participants increases, the number of matches grows quadratically, reflecting O(n²) complexity.
Common Misconceptions
Clarifying prevalent misunderstandings can deepen comprehension:
-
Big O Represents Exact Performance: A common misconception is that Big O notation provides the exact runtime of an algorithm. In reality, it describes the upper bound of an algorithm’s growth rate, indicating how performance scales with input size, not precise execution time.
-
Lower Big O Always Means Better Performance: While algorithms with lower time complexities generally perform better with large inputs, this isn’t universally true. Factors like constant factors and lower-order terms can make an algorithm with higher complexity more efficient for smaller datasets.
-
Big O is the only way to write time complexity: Big O notation describes the worst-case scenario, but variations of big O can describe it can also represent average and best-case complexities. However, worst-case analysis is typically emphasized to guarantee performance under all conditions.
-
You include coefficients: you can calculate with coeffficnets when doing calculations - for example if you have two loops sequentially after one another that would technically be O(2n) but in practice we right it as O(n) as at large timescales it becomes irrelevant.
Classwork Problems (Easy)
What is the time complexity of this function?
def sum_list(arr):
total = 0
for num in arr:
total += num
return total
Answer
O(n) – It loops through the list once.What is the time complexity of accessing an element in an array?
def get_element(arr, index):
return arr[index]
Answer
O(1) – Accessing an index takes constant time.What is the complexity of this nested loop?
def nested_loops(n):
for i in range(n):
for j in range(n):
print(i, j)
Answer
O(n²) – The inner loop runs `n` times for each iteration of the outer loop.Extra Practice Problems (Harder)
What is the time complexity of this function?
def reverse_string(s):
return s[::-1]
Answer
O(n) – It iterates through the string once to reverse it.What is the complexity of this function that removes duplicates?
def remove_duplicates(arr):
unique = set(arr)
return list(unique)
Answer
O(n) – Creating a set and list both take linear time.What is the time complexity of this function that checks for duplicates using a set?
def has_duplicates(arr):
seen = set()
for num in arr:
if num in seen:
return True
seen.add(num)
return False
Answer
O(n) – Each lookup and insertion in the set is O(1), and we loop through the list once.Why Does Big O Matter?
- Efficient algorithms save time & resources
- Choosing the right algorithm can make or break an application
- Helps in scaling up programs for large data
Case Study
1. Binary Search
- Big O Runtime: - O(log n) - The list is halved at each step, so it takes about log₂(n) operations.
- Number of Operations: - For a list with 100 million elements: - log₂(100,000,000) ≈ 26.6 operations.
- Estimated Runtime: - Assuming each operation takes ~0.1 microseconds: - 26.6 × 0.1 μs ≈ 2.66 μs (microseconds).
- Conditions: - List must be sorted for binary search to work. - Reduces search space by half each iteration.
2. Sequential Search (Linear Search)
- Big O Runtime: - O(n) - In the worst case, it scans the entire list.
- Number of Operations: - In the worst case, it checks all 100 million elements.
- Estimated Runtime: - Assuming each operation takes ~0.1 microseconds: - 100,000,000 × 0.1 μs = 10,000,000 μs = 10 seconds.
- Conditions: - Works for unsorted lists. - Can be faster if the element is found early.
Comparison Summary:
| Method | Big O | Number of Operations | Estimated Time |
|---|---|---|---|
| Binary Search | O(log n) | ~27 operations | ~2.7 microseconds |
| Sequential Search | O(n) | 100 million operations | ~10 seconds |
The time difference between 2.7 microseconds and 10 seconds is approximately 3.7 million times or about 6 orders of magnitude
How to Analyze Code for Time Complexity
When analyzing code for time complexity, ask yourself:
- Are there loops?
- A single loop over
nelements is usually O(n) - Nested loops often indicate O(n²) or worse
- A single loop over
- Are there recursive calls?
- Recursion can be O(n), O(log n), or O(2ⁿ) depending on how many times the function calls itself and how the input size shrinks
- Are there function calls inside loops?
- Watch out for things like
list.append()(O(1)) vs.list.insert(0, x)(O(n))
- Watch out for things like
- Are we accessing data structures?
- Accessing:
- Array/List element → O(1)
- Dictionary/Set lookup → O(1)
- Searching/sorting may be more expensive
- Accessing:
- What’s the dominant term?
- Drop constants and less significant terms (e.g.,
O(n + n²)becomes O(n²))
- Drop constants and less significant terms (e.g.,
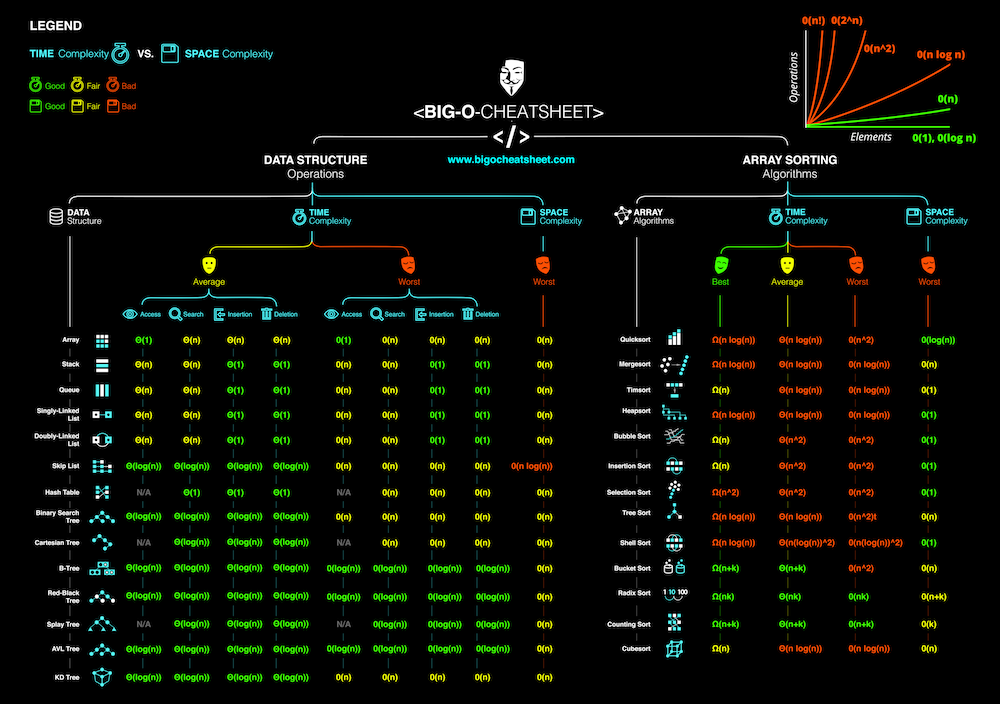
Space Complexity (brief)
Space complexity is how much extra memory your algorithm uses as input grows. The examples here are the most common ones but others do exist - much rarer in practice.
What to look for:
- New variables or data structures
- E.g.,
arr = [0] * n→ O(n)
- E.g.,
- Recursion
- Each recursive call adds to the call stack
- Input vs. Output
- Returning a new list instead of modifying the original list can increase space usage
Examples:
def double_list(nums):
return [x * 2 for x in nums]
- Space Complexity: O(n) – a new list is created
def in_place_double(nums):
for i in range(len(nums)):
nums[i] *= 2
- Space Complexity: O(1) – no new list, modifies in place
Rule of Thumbs:
- If you’re creating new lists, maps, or arrays, you’re using extra space → O(n)
- If you’re modifying in place or using a fixed number of variables → O(1)
MCQ Questions
Question 1
Question: A company delivers packages by truck and would like to minimize the length of the route that each driver must travel in order to reach n delivery locations. The company is considering two different algorithms for determining delivery routes.
Algorithm I Generate all possible routes, compute their lengths, and then select the shortest possible route. This algorithm does not run in reasonable time. Algorithm II Starting from an arbitrary delivery location, find the nearest unvisited delivery location. Continue creating the route by selecting the nearest unvisited location until all locations have been visited. This algorithm does not guarantee the shortest possible route and runs in time proportional to n^2.
Options:
- A: Algorithm II attempts to use an algorithmic approach to solve an otherwise undecidable problem.
- B: Algorithm II uses a heuristic approach to provide an approximate solution in reasonable time.
- C: Algorithm II provides no improvement over algorithm I because neither algorithm runs in reasonable time.
- D: Algorithm II requires a much faster computer in order to provide any improvement over algorithm I.
Answer: Option B Explanation: Algorithm II runs in time proportional to n^2, which is considered reasonable time because n^2 is a polynomial. This is considered a heuristic approach because it finds an approximate solution in reasonable time when the technique that finds an exact solution (algorithm I) does not run in reasonable time. Notes:
- Unreasonable time: An algorithm that runs in a time - that is simply not practical for use or breaks the systems in some way.
- Heurestic: A general guideline for something, heustics are oftne used when the problem is either unsolvable or just used as general rules to find a good answer (may not be perfect)
Rough Guidelines on Input Size
“Reasonable”:
-
O(1) Any size — instant -
O(log n) Millions — very efficient -
O(n) Up to ~10⁷ -
O(n log n) Up to ~10⁶ - 10⁷ -
O(n²) Up to ~10³ - 10⁴
“Unreasonable”:
-
O(2ⁿ) Usually breaks around n = 20-25 -
O(n!) Unreasonable after n = 10
Question 2
Question: Consider the following algorithms. Each algorithm operates on a list containing n elements, where n is a very large integer.
I. An algorithm that accesses each element in the list twice II. An algorithm that accesses each element in the list n times III. An algorithm that accesses only the first 10 elements in the list, regardless of the size of the list
Which of the algorithms run in reasonable time?
Options:
- A: I Only
- B: II Only
- C: I and II Only
- D: I, II, and III
Answer: Option D Explanation: For an algorithm to run in reasonable time, it must take a number of steps less than or equal to a polynomial function. Algorithm I accesses elements 2n times (twice for each of n elements), which is considered reasonable time. Algorithm II accesses n^2 elements (n times for each of n elements), which is considered reasonable time. Algorithm III accesses 10 elements, which is considered reasonable time. (Refer to table from Q1 for what’s generally considered “reasonable”) Notes:
- The concept of “unreasonable” is hard to define as it defines largely on the problem, the user, and the situation as in some scenarios, perhaps a run time of 5 seconds with a complexity of O(n^2) could be considered “unreasonable” if the input size is large for some usecases. But in other scenarios that same complexity and run time could be consdered “reasonable” - its largely based on the context. BUT for COLLEGEBOARD anythign until O(n^2) is typically considered reasonable.
Other types of “Algorithmic Efficiency Questions” (3.17):
- Will ask you to calculate the time difference between two algorithms given the amount of time it takes for one instance of the function to run, typically to find the answer just count/calculate the number of times that certain function is run and then perform basic arithmetic to find difference.
- Will be some variation of the problems we ahve shown above :)
Curious? Extensions of Big O
1. Big Omega Notation (Ω) – Best-Case Analysis
- Definition: Describes the lower bound of an algorithm’s running time, indicating the minimum amount of time required for the algorithm to complete for any input.
- When to Use: To identify the best possible performance of an algorithm.
- Example: Linear search: Ω(1) if the target element is found at the first position.
2. Big Theta Notation (Θ) – Average-Case Analysis
- Definition: Describes the tight bound of an algorithm’s running time, capturing both the upper and lower bounds. It represents the average case where the performance is neither best nor worst.
- When to Use: To analyze the most likely running time of an algorithm across all possible inputs.
- Example: Insertion sort: Θ(n²) for average case inputs where elements are neither fully sorted nor fully reversed.
3. Little O Notation (o) – Strict Upper Bound
- Definition: Describes an upper bound that is not tight, meaning the algorithm’s running time grows slower than the function provided.
- When to Use: To indicate that the running time will never grow as fast as the given function, even in the worst case.
- Example: An algorithm with time complexity o(n²) runs slower than O(n²), but faster than O(n³).
4. Little Omega Notation (ω) – Strict Lower Bound
- Definition: Describes a lower bound that is not tight, meaning the running time grows faster than the given function.
- When to Use: To show that the algorithm’s growth rate will always exceed the given function.
- Example: An algorithm with time complexity ω(n) grows faster than O(n) but slower than O(n²).
Homework
- Kahoot (07630957): https://kahoot.it/challenge/07630957?challenge-id=a5056a83-73e5-4bc2-9074-45da0014a0a1_1745191880417
- Homework Form Link: https://forms.gle/8yi5Rwv1HBEFJi1FA