Binary Systems & Logic Gates

Understanding Binary: The Foundation of Computing

Binary (Base-2) is the fundamental language of all computing systems. Unlike our familiar decimal system that uses ten digits (0-9), binary uses only two digits: 0 and 1. This elegantly maps to the physical reality of computers, where components can exist in one of two states: OFF (0) or ON (1).

Why Computers Use Binary

Physical Implementation: Electronic circuits have two stable states (high/low voltage)
Error Detection: Binary is less prone to noise and signal degradation
Processing Efficiency: Binary operations can be implemented with simple logic gates
Scalability: Complex systems can be built from simple binary building blocks

Number Systems Comparison

Base	Name	Digits Used	Example (15₁₀)	Common Uses
2	Binary	0-1	1111	Computer processing, digital storage
8	Octal	0-7	17	Legacy systems, file permissions
10	Decimal	0-9	15	Human calculations, everyday use
16	Hexadecimal	0-9, A-F	F	Memory addresses, color codes, debugging

Binary to Decimal Conversion

To convert a binary number to decimal:

Identify the place value of each bit (powers of 2 from right to left)
Multiply each bit by its place value
Sum all the results

binary

Example: Converting 10110₂ to decimal

1 × 2⁴ = 16
0 × 2³ = 0
1 × 2² = 4
1 × 2¹ = 2
0 × 2⁰ = 0
Sum: 16 + 0 + 4 + 2 + 0 = 22₁₀

Decimal to Binary Conversion

To convert a decimal number to binary:

Divide the number by 2
Note the remainder (0 or 1)
Continue dividing the quotient by 2 until you reach 0
Read the remainders bottom-to-top

Example: Converting 45₁₀ to binary

45 ÷ 2 = 22 remainder 1
22 ÷ 2 = 11 remainder 0
11 ÷ 2 = 5 remainder 1
5 ÷ 2 = 2 remainder 1
2 ÷ 2 = 1 remainder 0
1 ÷ 2 = 0 remainder 1
Result: 101101₂

Binary Arithmetic

Addition

  1 1 1    (carries)
  1 0 1 1  (11 in decimal)
+ 0 1 1 0  (6 in decimal)
---------
  1 0 0 0 1  (17 in decimal)

Rules:

0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0, carry 1
1 + 1 + 1 = 1, carry 1

Subtraction

  1 0 1 0  (10 in decimal)
- 0 0 1 1  (3 in decimal)
---------
  0 1 1 1  (7 in decimal)

Rules:

0 - 0 = 0
1 - 0 = 1
1 - 1 = 0
0 - 1 = 1 (after borrowing 1 from the left)

Two’s Complement: Representing Negative Numbers

Two’s complement is an elegant method computers use to represent and process negative numbers.

To convert a positive binary number to its negative equivalent:

Invert all bits (0→1, 1→0)
Add 1 to the result

Example: Converting +9₁₀ to -9₁₀ (using 8 bits)

+9₁₀ = 00001001₂
Invert: 11110110
Add 1: 11110111 = -9₁₀ in two’s complement

This approach allows computers to:

Use the same hardware for addition and subtraction
Represent positive and negative numbers seamlessly
Have only one representation of zero (00000000)

Bit Shifting Operations

Left Shift («)

Shifting bits left by n positions multiplies the number by 2ⁿ. Each bit moves n positions to the left, and 0s are filled in from the right.

Example: 00001010 « 2 = 00101000 (10₁₀ → 40₁₀)

Right Shift (»)

Shifting bits right by n positions divides the number by 2ⁿ (integer division). Each bit moves n positions to the right, and the leftmost bit is determined by the sign bit in signed numbers.

Example: 00101000 » 2 = 00001010 (40₁₀ → 10₁₀)

Logic Gates: The Building Blocks of Computing

Logic gates are the fundamental building blocks of all digital systems. They implement Boolean functions, processing binary inputs to produce binary outputs according to specific rules.

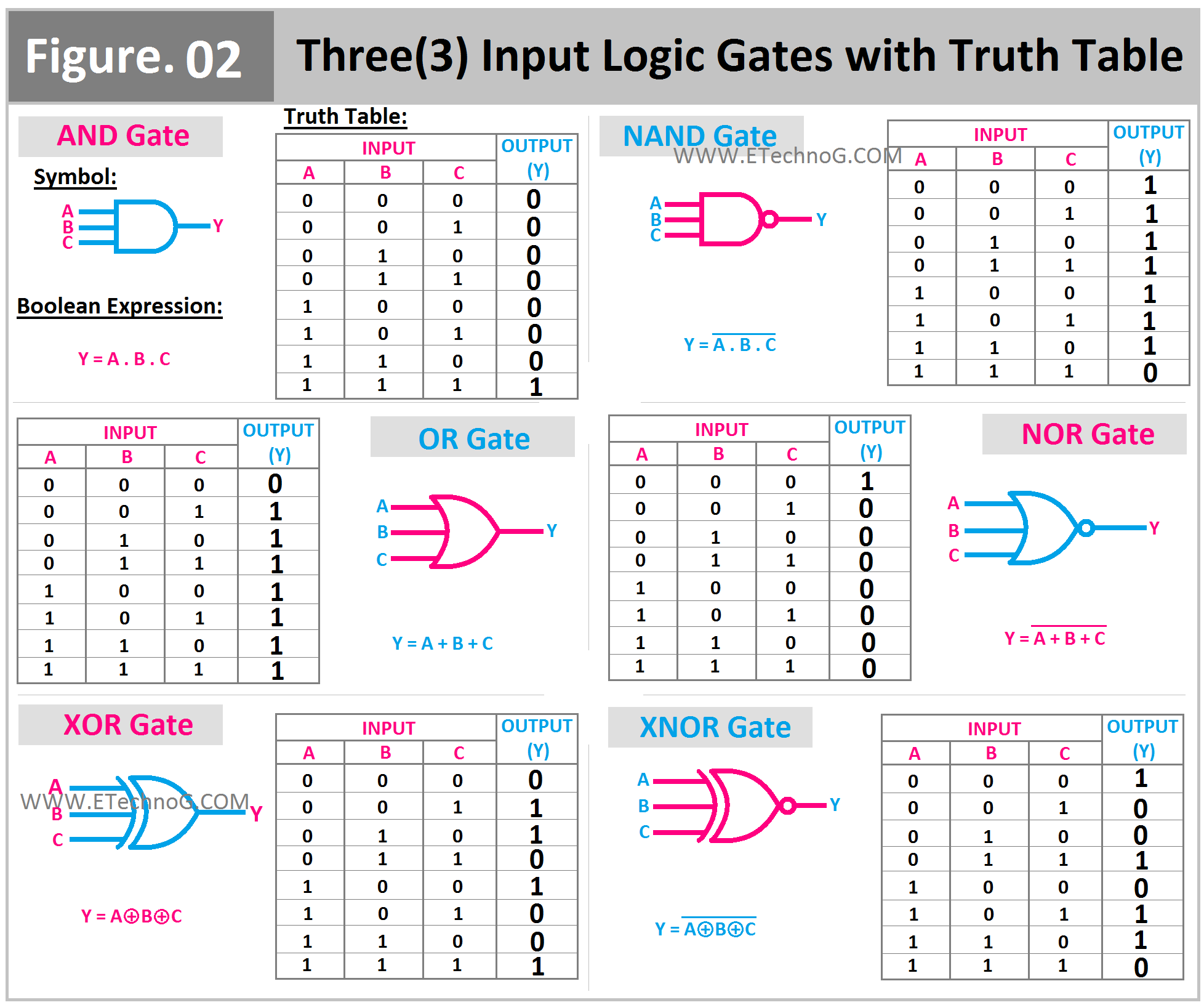
logic

Basic Logic Gates

AND Gate

Output is TRUE (1) only if ALL inputs are TRUE (1)
Analogous to the logical “and” operation
Symbol: AND Gate (resembles a D-shape with straight edge on output side)

Truth Table: | A | B | A AND B | |—|—|———| | 0 | 0 | 0 | | 0 | 1 | 0 | | 1 | 0 | 0 | | 1 | 1 | 1 |

Real-world analogy: A series circuit with two switches - both must be closed for the light to turn on.

Python implementation:

def AND(A, B):
    return A and B

# Example usage
print(AND(True, False))  # Output: False
print(AND(True, True))   # Output: True

OR Gate

Output is TRUE (1) if AT LEAST ONE input is TRUE (1)
Analogous to the logical “or” operation
Symbol: OR Gate (resembles a curved D-shape with pointed end at output)

Truth Table: | A | B | A OR B | |—|—|——–| | 0 | 0 | 0 | | 0 | 1 | 1 | | 1 | 0 | 1 | | 1 | 1 | 1 |

Real-world analogy: A parallel circuit with two switches - either one can be closed to turn on the light.

Python implementation:

def OR(A, B):
    return A or B

# Example usage
print(OR(True, False))  # Output: True
print(OR(False, False)) # Output: False

NOT Gate

Output is the INVERSE of the input
Analogous to the logical “not” operation
Symbol: NOT Gate (triangle with small circle at output)

Truth Table: | A | NOT A | |—|——-| | 0 | 1 | | 1 | 0 |

Real-world analogy: A normally-closed relay that opens when energized.

Python implementation:

def NOT(A):
    return not A

# Example usage
print(NOT(True))   # Output: False
print(NOT(False))  # Output: True

Compound Logic Gates

XOR Gate (Exclusive OR)

Output is TRUE (1) if EXACTLY ONE input is TRUE (1)
Useful for parity checking and binary addition
Symbol: XOR Gate (resembles OR gate with additional line)

Truth Table: | A | B | A XOR B | |—|—|———| | 0 | 0 | 0 | | 0 | 1 | 1 | | 1 | 0 | 1 | | 1 | 1 | 0 |

Python implementation:

def XOR(A, B):
    return (A or B) and not (A and B)
    # Alternatively: return A != B

# Example usage
print(XOR(True, True))   # Output: False
print(XOR(True, False))  # Output: True

NAND Gate (NOT AND)

Output is FALSE (0) only if ALL inputs are TRUE (1)
Universal gate - can implement any Boolean function
Symbol: NAND Gate (AND gate with small circle at output)

Truth Table: | A | B | A NAND B | |—|—|———-| | 0 | 0 | 1 | | 0 | 1 | 1 | | 1 | 0 | 1 | | 1 | 1 | 0 |

Python implementation:

def NAND(A, B):
    return not (A and B)

# Example usage
print(NAND(True, True))   # Output: False
print(NAND(False, True))  # Output: True

Logic Gates in Real Computer Components

Logic gates are combined to create:

Flip-flops: Basic memory elements that store a single bit
Registers: Groups of flip-flops that store multi-bit values
Multiplexers: Circuits that select between multiple inputs
Arithmetic Logic Units (ALUs): Process arithmetic and logical operations
Memory Controllers: Manage access to RAM and storage
CPU Control Units: Coordinate processing operations

Practical Applications of Binary and Logic Gates

Digital Electronics

Logic gates are the building blocks for all digital circuits. Your smartphone’s processor contains billions of transistors organized into logic gates that perform calculations by manipulating binary data.

Computer Memory

Every byte of RAM in your computer is a collection of binary digits (bits). Each bit is essentially a tiny electronic circuit that can be either ON (1) or OFF (0).

Digital Security

Binary powers modern cryptography through:

Password hashing using XOR operations
Digital signatures that use binary operations
Encryption algorithms that manipulate binary data

Real-world Control Systems

Industrial control systems use binary logic to:

Control traffic lights (IF condition THEN action)
Operate elevators using logic gate circuits
Manage automated manufacturing systems

Binary in Software Development

def validate_password(password):
    has_uppercase = any(char.isupper() for char in password)
    has_lowercase = any(char.islower() for char in password)
    has_digit = any(char.isdigit() for char in password)
    is_long_enough = len(password) >= 8
    
    # This uses logical AND: all conditions must be TRUE
    is_valid = has_uppercase and has_lowercase and has_digit and is_long_enough
    
    if not is_valid:
        if not (has_uppercase or has_lowercase):
            return "Password needs both uppercase and lowercase letters"
        elif not has_digit:
            return "Password needs at least one digit"
        elif not is_long_enough:
            return "Password must be at least 8 characters"
    
    return "Password is valid"

Feedback Image

Binary Calculator Implementation

Homework is to create a nice calculator that will work for Binary
Should have a conversion from decimal (0.1 extra credit)